
Phương pháp phần tử hữu hạn FEM
Mục lục
1/ FEM là gì ?
Phương pháp phần tử hữu hạn (FEM), là một phương pháp số gần đúng để giải các bài toán về kỹ thuật và vật lí toán học.Các vấn đề được quan tâm bao gồm phân tích kếtcấu, truyền nhiệt, lưu chất, truyền khối và điện thế.
Phương pháp giải tích cho bài toán thường đòi hỏi giải pháp cho bài toán giá trị biên cho phương trình vi phân từng phần. Phương thức phần tử hữu hạn xây dựng kết quả bài toán trong một hệ phương trình đại số. Phương thức này đưa ra các giá trị gần đúng của các ẩn tại một số phần tử rời rạc trên miền xác định.[1] Để giải bài toán, chia nhỏ nó thành nhiều miền con (phần tử), đơn giản hơn được gọi là các phần tử hữu hạn. Các phương trình đơn giản mô hình hóa các phần tử hữu hạn này sau đó được tập hợp thành một hệ phương trình lớn hơn mô hình hóa toàn bộ vấn đề.Sau đó, FEM sử dụng các phương pháp biến đổi từ phép tính các biến thể để giải hệ phương trình này sẽ tìm được các giá trị của hàm xấp xỉ tại các điểm nút của mỗi phần tử, nhờ đó hàm xấp xỉ hoàn toàn được xác định trên mỗi một phần tử.
Nghiên cứu hoặc phân tích hiện tượng với FEM thường được gọi là phân tích phần tử hữu hạn (FEA).
1.1/ Lịch sử ra đời và phát triển
Phương pháp phần tử hữu hạn bắt nguồn từ sự cần thiết phải giải quyết các bài toán phức tạp về lý thuyết đàn hồi, phân tích kết cấu trong xây dựng và kỹ thuật hàng không. Nó được bắt đầu và phát triển bởi A. Hrennikoff [4] và R. Courant [5] vào đầu những năm 1940. Một nhà tiên phong khác là Ioannis Argyris. Ở Liên Xô, sự ra đời của ứng dụng thực tế của phương pháp này thường được nhắc đến với tên của Leonard Oganesyan. [6] Ở Trung Quốc, vào những năm 1950 và đầu những năm 1960, dựa trên tính toán các công trình đập, K. Feng đã đề xuất một phương pháp số có hệ thống để giải các phương trình vi phân từng phần. Phương pháp này được gọi là phương pháp sai phân hữu hạn dựa trên nguyên tắc biến đổi, đó là một phát minh độc lập khác của phương pháp phần tử hữu hạn. Mặc dù các phương pháp tiếp cận được sử dụng bởi những người tiên phong này là khác nhau, họ đều có chung một quan điểm: chia lưới của một miền liên tục thành một tập hợp các tên miền con rời rạc, thường được gọi là các phần tử.
Hrennikoff rời rạc hóa miền liên tục bằng cách sử dụng lưới tương tự, trong khi Courant chia lưới tam giác cho cách giải thứ hai của phương trình vi phân từng phần (PDEs) nó được phát sinh từ bài toán xoắn của một hình trụ. Đóng góp của Courant là là một bước tiến, từ kết quả trước đó cho các PDE được phát triên bởi Rayleigh, Ritz và Galerkin.
Phương pháp phần tử hữu hạn chính thức phát triển trong những năm 1960 và 1970 bởi sự mở rộng của JH Argyris với đồng nghiệp tại Đại học Stuttgart, RW Clough với đồng nghiệp tại UC Berkeley, OC Zienkiewicz với đồng nghiệp Ernest Hinton, Bruce Irons và những người khác tại Đại học Swansea, Philippe G. Ciarlet tại Đại học Paris 6 và Richard Gallagher cùng với các đồng nghiệp tại Đại học Cornell. Nhiều sự phát minh mới đã được đưa ra trong những năm này với sự có sẵn của những phần mềm mở có gái trị. NASA tài trợ phiên bản gốc của NASTRAN, UC Berkeley triển khai Chương trình Phần tử hữu hạn SAP IV một cách rộng rãi. Tại Na Uy, Det Norske Veritas (nay là DNV GL) đã phát triển Sesam vào năm 1969 để sử dụng trong phân tích tàu thủy. Một cơ sở toán học nghiêm ngặt cho phương pháp phần tử hữu hạn được cung cấp vào năm 1973 bằng việc xuất bản Strang và Fix. Phương pháp này đã được khái quát hóa để mô hình hóa lượng lớn phương pháp vật lý trong nhiều ngành kỹ thuật khác nhau, ví dụ như điện từ, truyền nhiệt và động lực học chất lỏng.
2/ Ứng dụng
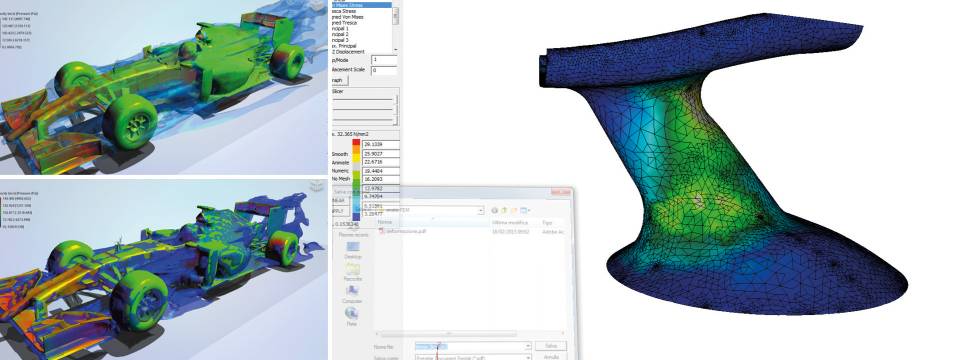
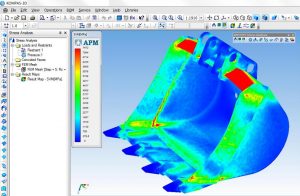
Một loạt các chuyên ngành thuộc lĩnh vực kĩ thuật cơ khí (như ngành hàng hông, cơ khí, ô tô,..) thường sử dụng FEM tích hợp trong thiết kế và phát triển sản phẩm. Một số phần mềm FEM hiện đại bao gồm các thành phần cụ thể như môi trường làm việc nhiệt, điện từ, chất lỏng và cấu trúc. Trong một mô phỏng cấu trúc, FEM giúp rất nhiều trong việc tạo ra độ cứng và ứng suất và cũng như trong việc giảm thiểu trọng lượng, vật liệu và chi phí.
FEM cho phép hình dung chi tiết về các cấu trúc uốn cong hoặc xoắn, chỉ ra sự phân bố ứng suất và chuyển vị. Phần mềm FEM cung cấp một loạt các tùy chọn mô phỏng để kiểm soát sự phức tạp của cả mô hình hóa và phân tích của một hệ thống. Tương tự, mức độ mong muốn về độ chính xác cần thiết và các yêu cầu về thời gian tính toán liên quan có thể được quản lý đồng thời để giải quyết hầu hết các ứng dụng kỹ thuật. FEM cho phép toàn bộ các thiết kế được xây dựng, tinh chế và tối ưu hóa trước khi thiết kế được sản xuất.
FEM đã cải thiện đáng kể các tiêu chuẩn thiết kế kĩ thuật và phương pháp, quá trình thiết kế trong nhiều ứng dụng của công nghiệp. Làm giảm đáng kể thời gian để đưa một sản phẩm từ khái niệm vào sản xuất. Tóm lại lợi ích khi sử dụng FEM gồm độ chính xác cao, hiểu rõ các thông số thiết kế quan trọng, tạo mẫu ảo, ít tốn phần cứng, chu trình thiết kế nhanh hơn, ít tốn kém hơn, tăng năng suất và doanh thu.
3/ Các khái niệm cơ bản
Chia nhỏ những miền liên tục thành những miền con rời rạc có một số ưu điểm:
- Biểu diễn chính xác hình học phức tạp
- Bao hàm các thuộc tính vật liệu không giống nhau
- Dễ dàng biểu diễn giải pháp cụ thể
- Ghi lại phản ứng cục bộ
Một công việc điển hình trong phương pháp này bao gồm phân chia miền của vấn đề thành một tập hợp các tên miền phụ, với mỗi tên miền phụ được biểu diễn bằng một tập hợp các phương trình phần tử cho bài toán gốc, sau đó (2) hệ thống kết hợp lại tất cả các phương trình phần tử vào một hệ phương trình tuyến tính cho phép tính cuối cùng. Hệ phương trình tuyến tính đã biết cách giải, và có thể được tính toán từ các giá trị ban đầu của bài toán gốc để có được một câu trả lời bằng số.
Trong bước đầu tiên ở trên, các phương trình phần tử là các phương trình đơn giản mà xấp xỉ so với phương trình phức tạp ban đầu được nghiên cứu, trong đó các phương trình ban đầu thường là phương trình vi phân từng phần (PDE). Để giải thích sự xấp xỉ đó, phương pháp phần tử hữu hạn (FEM) thường được giới thiệu như một trường hợp đặc biệt của phương pháp Galerkin. Quá trình này trong ngôn ngữ toán học là để xây dựng một tích phân của tích số bên trong của số dư và hàm trọng số và thiết lập tích phân bằng 0. Nói một cách đơn giản, nó là một phương pháp giảm thiểu sai số xấp xỉ bằng cách gắn các hàm thử nghiệm vào PDE. Phần còn lại là lỗi do các hàm thử nghiệm gây ra, và các hàm trọng số là các hàm xấp xỉ đa thức dự tính số dư. Quá trình loại bỏ tất cả các dẫn xuất không gian từ PDE, do đó xấp xỉ PDE cục bộ với:
- Một tập hợp các phương trình đại số cho các vấn đề trạng thái ổn định
- Một tập hợp các phương trình vi phân thông thường cho các vấn đề nhất thời
Các phương trình này là các phương trình phần tử. Chúng là tuyến tính nếu PDE cơ bản là tuyến tính và ngược lại. Các phương trình đại số phát sinh trong các bài toán trạng thái ổn định được giải bằng phương pháp đại số tuyến tính số, trong khi các phương trình vi phân thường phát sinh trong các vấn đề tạm thời được giải quyết bằng tích phân số bằng các kỹ thuật tiêu chuẩn như phương pháp Euler hoặc phương pháp Runge-Kutta.
Trong bước (2) ở trên, một hệ phương trình tuyến tính được tạo ra từ các phương trình phần tử thông qua việc chuyển đổi các tọa độ từ các nút cục bộ của các tên miền phụ sang các nút toàn cục của miền. Sự chuyển đổi không gian này bao gồm các điều chỉnh định hướng thích hợp như được áp dụng liên quan đến hệ tọa độ tham chiếu. Quá trình này thường được thực hiện bởi phần mềm FEM bằng cách sử dụng dữ liệu tọa độ được tạo ra từ các tên miền phụ.
FEM được hiểu rõ nhất từ ứng dụng thực tế của nó, được gọi là phân tích phần tử hữu hạn (FEA). FEA được áp dụng trong kỹ thuật như là một công cụ tính toán để thực hiện phân tích kỹ thuật. Nó bao gồm việc sử dụng kỹ thuật tạo lưới để phân chia một miền phức tạp thành các phần tử nhỏ, cũng như việc sử dụng chương trình phần mềm được mã hóa bằng thuật toán FEM. Khi áp dụng FEA, vấn đề phức tạp thường là một hệ vật lý với cơ sở dựa vào phương trình chùm Euler-Bernoulli, phương trình nhiệt, hoặc phương trình Navier-Stokes thể hiện trong cả hai phương trình tích phân hoặc PDE, trong khi chia nhỏ phần tử của vấn đề phức tạp đại diện cho các khu vực khác nhau trong hệ thống vật lý.
FEM là lựa chọn tốt để phân tích các bài toán trên các miền phức tạp (như ô tô, đường ống dẫn dầu,…), khi miền thay đổi (như trong một phản ứng trạng thái với biên thay đổi), khi độ chính xác kì vọng thay đổi trên toàn bộ miền hoặc khi giải pháp thiếu độ mịn. Mô phỏng FEA cung cấp một nguồn tài nguyên có giá trị khi chúng loại bỏ trường hợp tạo và thử nghiệm các mẫu thử cứng cho các tình huống độ trung thực cao khác nhau. Ví dụ, trong một mô phỏng tai nạn ở phía trước có thể tăng độ chính xác dự đoán trong các khu vực “quan trọng” như mặt trước của xe và giảm nó ở phía sau của nó (do đó làm giảm chi phí của mô phỏng). Một ví dụ khác là ứng dụng trong dự báo thời tiết, nơi quan trọng hơn để có những dự đoán chính xác về việc phát triển các hiện tượng phi tuyến cao (chẳng hạn như lốc xoáy nhiệt đới trong khí quyển, hoặc xoáy trong đại dương) thay vì các khu vực tương đối yên tĩnh.
4/ Thảo luận khoa học
4.1/ Cấu trúc của các phương pháp phần tử hữu hạn
Phương pháp phần tử hữu hạn là phương pháp số cho lời giải xấp xỉ của các bài toán trong toán học, tức là thường được phát biểu một cách có hệ thống để nêu chính xác tình trạng của một số khía cạnh trong thực tế của vật lý.
Một phương pháp phần tử hữu hạn được đặc trưng bởi một công thức biến đổi, một sự rời rạc hóa, hoặc nhiều thuật toán giải pháp và các quy trình hậu xử lý.
Ví dụ cho công thức biến đổi là phương pháp Galerkin, phương pháp Galerkin gián đoạn, phương pháp hỗn hợp, …
Sự rời rạc hóa được định nghĩa gồm một tập hợp các bước được xác định rõ ràng gồm:
- Tạo ra các phần tử hữu hạn
- Định nghĩa hàm cơ sở trên các phần tử tham chiếu (hàm hình dạng)
- Ánh xạ tham chiếu các phần tử lên lưới
Ví dụ về sự rời rạc hóa là h-version, p-version, hp-version, x-FEM, phân tích đẳng hình học,…Mỗi phương pháp rời rạc hóa đều có một số thuận lợi và bất lợi. Tiêu chuẩn hợp lí trong việc lựa chọn phương pháp rời rạc hóa là để đạt được hiệu suất tối ưu cho tập hợp rộng nhất của các mô hình trong một mô hình cụ thể.
Có hai loại thuật toán giải pháp rộng:
- Giải quyết trực tiếp
- Lặp đi lặp lại
Các thuật toán này được thiết kế để khai thác ma trận thưa phụ thuộc vào sự lựa chọn của công thức biến đổi và sự rời rạc hóa.
Thủ tục sau xử ký được thiết kế để trích xuất dữ liệu cần thiết từ giải pháp phần tử hữu hạn, Để đáp ứng yêu cầu của việc xác minh sự chính xác của giải pháp, các nhà xử lý cần phải cung cấp một ước lỗi chuẩn về mặt vấn đề đang được quan tâm. Khi các lỗi xấp xỉ lớn hơn những gì được coi là chấp nhận được thì việc lọc phải được thay đổi bằng quy trình thích nghi tự động hoặc theo ý của nhà phân tích. Có một số bộ xử lý rất hiệu quả cung cấp cho phương pháp siêu hội tụ.
4.2/ Các vấn đề minh họa P1 và P2
Minh họa việc sử dụng PPPTHH từ hai ví dụ mà phương pháp chung có thể là ngoại suy. Xem như người đọc đã quen thuộc với đại số tuyến tính:
P1 là bài toán một chiều
Sử dụng bài toán một chiều, tại đây, hàm f được xác định bởi u và u một hàm ẩn của x, u’’ là đạo hàm cấp 2 của u theo x
P2 là bài toán hai chiều
Miền Ω là một miền đơn liên mở trong mặt phẳng (x,y), có biên ∂Ω rất “đẹp” (ví dụ: một đa tạp trơn hoặc một đa giác), {\displaystyle u_{xx}}uxx và uyy {\displaystyle u_{yy}} là đạo hàm riêng cấp hai theo biến x và y.
Ở ví dụ P1, có thể giải trực tiếp bằng cách lấy nguyên hàm. Tuy nhiên, phương pháp này chỉ thực hiện được trong không gian một chiều và không thể giải được trong không gian có hơn hai chiều hoặc trong bài toán u + u’’ = f. Chính vì lý do này mà chúng ta sẽ phát triển phát triển FEM cho trường hợp P1 và phác họa tổng quát của FEM cho trường hợp P2.
Lời giải gồm hai bước, nó phản ánh hai bước chủ yếu phải thực hiện để giải một bài toán biên bằng FEM. Ở bước đầu tiên, chúng ta sẽ biểu diễn lại bài toán biên trong dạng gần đúng của nó hoặc dạng biến phân. Rất ít hoặc không có máy tính được dùng để thực hiện bước này, việc này được làm bằng tay ở trên giấy. Bước thứ hai là rời rạc hóa, dạng gần đúng được rời rạc trong một không gian hữu hạn chiều. Sau bước thứ hai này, chúng ta sẽ có biểu thức cụ thể cho toàn bộ bài toán nhưng lời giải của bài toán trong không gian hữu hạn chiều tuyến tính chỉ là lời giải gần đúng của bài toán biên. Bài toán trong không gian hữu hạn chiều này sau đó được giải bằng máy tính.
4.3/ Công thức yếu
Bước đầu tiên là chuyển đổi P1 và P2 thành công thức yếu tương đương của chúng.
Công thức yếu của P1
Nếu u giải P1 thì đối với bất kỳ hàm trơn v nào thỏa mãn điều kiện chuyển vị, v=0 khi x=0 và x=1, ta có:
Ngược lại, nếu u với u(0)=u(1)=0 thì thỏa mãn (1) cho hàm trơn v(x) sau đó ta có thể thấy là u sẽ giải được P1. Thử dễ dàng hơn đối với hai lần hàm khả vi u (định lí giá trị trung bình), nhưng cũng có thể được chứng minh theo phương phân bố.
Định nghĩa một hàm mới bằng cách sử dụng tích hợp theo các phần ở bên tay phải của (1):
Với v(0)=v(1)=0
Công thức yếu của P2
Nếu lấy tích phân từng phần bằng công thức Green, ta có thể giải được P2 bằng u, nếu định nghĩa cho bất kỳ v
Trong đó, được định nghĩa là gradient và “.” là dấu chấm trong mặt phẳng hai chiều. Một lần nữa có thể quay về làm tích số trên không gian thích hợp của hàm vi phân một lần của bằng không trên . Chúng ta giả định rằng . Biển diễn được sự tồn tại và tính duy nhất của giải pháp,
4.3/ Sự rời rạc hóa
P1 và P2 đã sẵn sàng để được cụ thể hóa, dẫn đến một bài toán phụ phổ biến (3). Ý tưởng cơ bản là thay thế bài toán tuyến tính:
Tìm sao cho
Với một phiên bản hữu hạn chiều:
Tìm sao cho
trong đó V là một không gian con hữu hạn chiều của . Có nhiều sự lựa chọn có thể cho V (một khả năng dẫn đến phương pháp quang phổ). Tuy nhiên, đối với phương thức phần tử hữu hạn, chúng ta lấy V để là một không gian của các hàm đa thức từng phần.
Cho bài toán P1
Lấy khoảng(0,1), chọn giá trị n của x với: và định nghĩa V bằng: v liên tục, là tuyến tính, cho k=0,…n,a
Trong đó, ta định nghĩa x0=0 và xn+1=1. QUan sát các hàm trong V không khác biệt theo định nghĩa cơ bản của phép tính. Thật vậy, nếu thì đạo hàm không được xác định tại bất kì điểm nào ngoài x=xk, k=1,…n. Tuy nhiên, đạo hàm tồn tại ở mọi giá trị khác của x và có thể sử dụng đạo hàm này cho mục đích tích phân theo từng phần.
Cho bài toán P2
Chúng ta cần V là một tập các hàm của . Trong hình bên phải, chúng tôi đã minh họa một hình tam giác của một vùng đa giác 15 trong mặt phẳng (bên dưới), và một hàm tuyến tính từng mẩu (trên, màu) của đa giác này là tuyến tính trên mỗi tam giác của phép đạc tam giác; không gian V sẽ bao gồm các hàm tuyến tính trên mỗi tam giác của phép đạc tam giác đã chọn.
Hy vọng rằng khi lưới tam giác bên dưới trở nên mịn hơn thì lời giải của bài toán rời rạc theo ý nghĩa nào nó sẽ xấp xỉ với đáp án của bài toán giá trị biên ban đầu P2.Để đo độ mịn của lưới này, phép đạc tam giác được lập chỉ mục bởi một tham số có giá trị thực với giá trị rất nhỏ. Tham số này sẽ liên quan đến kích thước của tam giác lớn nhất hoặc trung bình trong tam giác. Khi ta chỉnh phép đạc tam giác , không gian của các hàm tuyến tính liên kết V phải thay đổi theo h. Vì lí do này, thường đọc Vh thay vì V trong tài liệu.
Chọn một cơ sở
Để hoàn thành việc rời rạc hóa, chúng ta phải chọn một cơ sở của V. Trong trường hợp một chiều, cho mỗi điểm kiểm soát xk, chúng tôi sẽ chọn hàm tuyến tính từng phần vk trong V của giá trị 1 tại xk và 0 tại mọi xj, j khác k
Cho k=1,…n; cơ sở này là một hàm tăng. Đối với trường hợp hai chiều, chọn lại một hàm cơ sở vk trên mỗi đỉnh xk của tam giác hai chiều . Hàm vk là hàm đơn giản của V có giá trị là 1 tại xk và 0 tại mỗi xj,j khác k.
Tùy thuộc vào người dùng, từ “phần tử” trong “phương thức phần tử hữu hạn” đề cập đến các tam giác trong miền, hàm cơ bản tuyến tính từng phần hoặc cả hai. Vì vậy, ví dụ, một người dùng quan tâm đến các lĩnh vực mặt cong có thể thay thế các hình tam giác bằng hình tròn, và do đó có thể mô tả các yếu tố như là curvilinear. Mặt khác, một số tác giả thay thế “tuyến tính từng phần ” bằng “bậc hai từng phần” hoặc thậm chí “đa thức từng phần”. Người dùng sau đó có thể nói “phần tử bậc cao hơn” thay vì “đa thức bậc cao”. Phương thức phần tử hữu hạn không bị giới hạn trong tam giác (hoặc tứ diện trong 3-d, hoặc đơn vị bậc cao hơn trong không gian đa chiều), nhưng có thể được định nghĩa trên các tên miền phụ tứ giác (lục giác, lăng kính, hoặc kim tự tháp trong 3-d, vv). Các hình dạng bậc cao hơn (các phần tử đường cong) có thể được xác định bằng các hình đa thức và thậm chí không đa thức (ví dụ như hình elip hoặc hình tròn).
Ví dụ về các phương pháp sử dụng các hàm cơ sở đa thức bậc cao hơn là hp-FEM và spectral FEM.
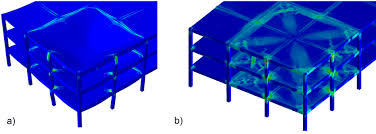
Các triển khai nâng cao hơn (phương pháp phần tử hữu hạn thích nghi) sử dụng một phương pháp để đánh giá chất lượng của các kết quả (dựa trên lý thuyết ước lượng lỗi) và sửa đổi lưới trong giải pháp nhằm đạt được giải pháp gần đúng trong một số giới hạn từ giải pháp ‘chính xác’ vấn đề. Lưới thích ứng có thể sử dụng các kỹ thuật khác nhau, phổ biến nhất là:
- Các nút chuyển động (r-adaptivity)
- Tinh chế (và không tinh chế) các phần tử (h-adaptivity)
- Thay đổi thứ tự của các hàm cơ sở (p-adaptivity)
- Sự kết hợp của các tính năng trên (hp-adaptivity).
Một vài hỗ trợ cơ sở
Ưu điểm chính của sự lựa chọn cơ sở này là các tích bên trong
Sẽ bằng 0 với hầu hết j, k. Ma trận chứa (vj,vk) trong (j,k) được gọi là ma trận Gramian. Trong trường hợp 1 chiều, vk được xác định trong khoảng . Sau đây, hàm lấy tích phân của (vj,vk) và (vj,vk) là giống hệt nhau khi và đều bằng 0.
Biểu mẫu của bài toán ma trận
Nếu ta viết và khi đó bài toán biết v(x)=vj(x) cho j=1,…,n trở thành cho j=1,…,n. Nếu chúng ta biểu diễn bằng u và f là các vector cột (u1,…un)t và (f1,…,fn)t và nếu ta cho L=(Lij) và M=(Mij) là ma trận có mục: và . Sau đó: -Lu=Mf. Nó không thực sự cần thiết để cho rằng . Đối với hàm tổng quát f(x) của bài toán với v(x)=vj(x) với j=1,…,n, trở nên đơn giản hơn vì không cần sử dụng ma trận M: -Lu=b với b=(b1,…,bn)t và , j=1,…,n.
Như chúng ta đã thảo luận từ trước, hầu hết các mục của L và M là bằng 0 vì hàm cơ sở vk có vùng hỗ trợ nhỏ. Vì vậy bây giờ chúng ta phải giải một hê tuyến tính trong khi không biết u hầu hết mục của ma trận L, ta cần nghịch đảo sau đó cho bằng 0.
Các ma trận này được gọi là ma trận thưa, và có các cách giải hiệu quả cho các bài toán như vậy (hiệu quả hơn nhiều so với nghịch đảo ma trận.) Ngoài ra, L là đối xứng và xác định dương, do đó, một phương pháp như phương pháp gradient liên hợp được ưa chuộng. Đối với các bài toán không quá lớn, LU decompositions và Cholesky decompositions vẫn hoạt động tốt. Ví dụ, toán tử dấu gạch chéo ngược của MATLAB (trong đó sử dụng LU decompositions và Cholesky decompositions, và các phương pháp hệ số hóa khác) có thể đủ cho các mắt lưới với một trăm nghìn đỉnh.
Ma trận L thường được gọi là ma trận độ cứng, trong khi ma trận M được gọi là ma trận khối lượng.
Dạng chung của phương pháp phần tử hữu hạn
Nói chung , phương pháp phần tử hữu hạn được đặc trưng bằng hai bước sau:
+ Chọn một dạng lưới cho . Lưới bao gồm hình tam giác, nhưng cũng có thể sử dụng hình vuông hoặc đa giác cong.
+ Sau đó chọn một hàm dạng cơ bản. Trong cuộc thảo luận, chúng ta đã sử dụng hàm từng phần tuyến tính cơ bản, nhưng hàm cơ sở đa thức cũng được sử dụng rất phổ biến.
Một vấn đề khác là sự mịn khi chia lưới của hàm cơ sở đa thức. Đối với bài toán về giá trị biên của eliptic bậc hai, hàm cơ sở đa thức chỉ đơn thuần là đáp ứng vừa đủ (tức là các đạo hàm không liên tục).Với phương trình vi phân từng phần bậc hai, cần phải sử dụng một hàm cơ sở mịn hơn. Ví dụ cho một bài toán khác như uxxxx+uyyyy=f, có thể sử dụng hàm cơ sở bậc hai là C1.
5/ Các loại phương pháp phần tử hữu hạn
5.1/ AEM
Phương pháp phần tử ứng dụng(AEM) kết hợp các tính năng của cả FEM và phướng pháp rời rạc hóa phần tử(DEM).
5.2/ Phương pháp phần tử hữu hạn tổng quát
Phương pháp phần tử hữu hạn tổng quát(GFEM) sử dụng không gian quỹ tích gồm có của hàm số, không cần thiết sử dụng đa thức, do đó phản ánh thông tin có sẵn về giải pháp chưa biết do đó đảm bảo xấp xỉ cục bộ tốt. Sau đó một bộ phận miền được sử dụng để lien kết các không gian này với nhau tạo thành khoogn gian con gần đúng. Hiệu quả của GFEM đã được thể hiện khi áp dụng cho các bài toán có đường biên phức tạp, các bài toán với quy mô nhỏ và các bài toán với các lớp ranh giới.
5.3/ Phương pháp phần tử hữu hạn hỗn hợp
Phương pháp phần tử hữu hạn hỗn hợp là một loại phương pháp phần tử hữu hạn trong đó các biến phụ độc lập được thêm vào dưới dạng các biến nút trong quá trình giải bài toán của một phương trình vi phân từng phần.
5.4/ hp-FEM
Phương pháp hp-FEM kết hợp linh động các phần tử với kích thước biến số h và bậc của đa thức p để đạt được tốc độ hội tụ theo cấp số mũ cực kì nhanh.
5.5/ hpk-FEM
Phương pháp hpk-FEM kết hợp linh động, các phần tử có kích thước biến số h, bậc đa thức của các xấp xỉ cục bộ p và tính đa dạng toàn cục của các xấp xỉ cục bộ (k-1) để đạt được tốc độ hội tụ tốt nhất
5.6/ XFEM
Phương pháp phần tử hữu hạn mở rộng (XFEM) là một bước tiến mới dựa trên phương pháp phần tử hữu hạn tổng quát (GFEM) và hàm phân bố thống nhất (PUM). Nó mở rộng phương pháp phần tử hữu hạn cổ điển bằng cách làm rộng không gian giải pháp cho các giải pháp cho các phương trình vi phân với các hàm không liên tục. Các phương thức phần tử hữu hạn mở rộng làm giàu không gian xấp xỉ để nó có thể tái tạo một cách tự nhiên tính năng đầy thử thách liên quan đến vấn đề quan tâm: sự gián đoạn, kỳ dị, lớp biên, v.v. tính năng vào khoảng không gian gần đúng có thể cải thiện đáng kể tốc độ hội tụ và độ chính xác. Hơn nữa, xử lý các vấn đề với sự gián đoạn với XFEMs ngăn cản việc lưới và làm lại các bề mặt gián đoạn, do đó làm giảm chi phí tính toán và các lỗi chiếu liên quan đến các phương pháp phần tử hữu hạn thông thường, với chi phí hạn chế sự gián đoạn đối với các cạnh lưới.
Một số nghiên cứu thực hiện kỹ thuật này với các mức độ khác nhau: GetFEM++2, xfem++3 và open fem ++
XFEM cũng đã được thực hiện trong các chương trình như Altair Radioss, ASTER, Morfeo và Abaqus. Nó ngày càng được chấp nhận bởi các phần tử phần tử hữu hạn thương mại khác, với một vài bổ sung và các triển khai lõi thực tế có sẵn (ANSYS, SAMCEF, OOFELIE, vv).
5.7/ Phương pháp phần tử hữu hạn tỷ lệ đường biên ( SBFEM )
Ra đời bởi Song và Wolf vào năm 1997. Là một trong những đóng góp có tác dụng to lớn trong lĩnh vực phân tích số liệu của cơ học phá hủy. Nó là một phương pháp tích phân cơ bản, có giải pháp kết hợp các ưu điểm của cả các công thức và quy trình phần tử hữu hạn, và sự rời rạc hóa. Tuy nhiên nó không yêu cầu lời giải vi phân cơ bản.
5.8/ S-FEM
Phương pháp phần tử hữu hạn S-FEM, Smoothed, là một lớp cụ thể của các thuật toán mô phỏng số để mô phỏng các hiện tượng vật lý. Nó được phát triển bằng cách kết hợp các phương thức chia lưới tự do với phương thức phần tử hữu hạn.
5.9/ Phương pháp phần tử quang phổ ( SEM )
Phương pháp phần tử quang phổ kết hợp tính linh hoạt hình học của các phần tử hữu hạn và độ chính xác cấp tính của các phương pháp phổ. Phương pháp quang phổ là giải pháp gần đúng của các phương trình từng phần yếu hình thành dựa trên nội suy bậc cao Lagragian và chỉ được sử dụng với các quy tắc bậc hai nhất định.
5.10/ Liên kết với phương pháp discretisation gradient
Một số loại phương pháp phần tử hữu hạn (phù hợp, không phù hợp, các phương thức phần tử hữu hạn hỗn hợp) là các trường hợp cụ thể của phương thức giải phóng gradient (GDM). Do đó các đặc tính hội tụ của GDM, được thiết lập cho một loạt các vấn đề (các vấn đề elliptic tuyến tính và phi tuyến tính, các vấn đề parabolic tuyến tính, phi tuyến và thoái hóa), giữ cho các phương pháp phần tử hữu hạn đặc biệt này.
5.11/ So sánh với phương pháp sai phân hữu hạn:
Phương pháp sai phân hữu hạn (FDM) là một cách thay thế xấp xỉ các giải pháp của PDE. Sự khác biệt giữa FEM và FDM là:
+ Tính năng hấp dẫn nhất của FEM là khả năng xử lý hình học phức tạp (và biên) một cách dễ dàng. Trong khi đó FDM căn bản chỉ áp dụng được trong các hình chữ nhật đơn giản, việc xử lý các bài toán hình học trong FEM về mặt lý thuyết là đơn giản hơn.
+ FDM thường không được sử dụng cho hình học CAD không thường xuyên nhưng thường là các mô hình hình chữ nhật hoặc mô hình khối.
+ FDM rất dễ làm
+ Có thể xem FDM là một trường hợp gần đúng của FEM. Những bước đầu tiên của FDM giống hệt FEM với phương trình Poisson, nếu bài toán rời rạc hóa bằng lưới hình chữ nhật với mỗi hình chữ nhật chia thành hai tam giác.
+ Có nhiều lý do để xem xét nền tảng toán học của phần tử hữu hạn xấp xỉ hợp lí nhiều hơn, ví dụ, bởi vì chất lượng của xấp xỉ giữa các điểm lưới là kém trong FDM.
+ Chất lượng của một FEM xấp xỉ thường cao hơn so với FDM xấp xỉ tương ứng, nhưng điều này lại phụ thuộc vào số hạng đầu của bài toán và một số trường hợp cho kết quả ngược lại.
Nói chung, FEM là phương pháp được lựa chọn trong tất cả các loại phân tích trong cơ học kết cấu (ví dụ giải quyết biến dạng và ứng suất trong vật rắn hoặc động lực học cấu trúc) trong khi động lực học chất lỏng (CFD) có xu hướng sử dụng FDM hoặc các phương pháp khác như phương pháp khối lượng hữu hạn ( FVM). Các vấn đề CFD thường đòi hỏi phải giải bài toán thành một số lượng lớn các ô / điểm lưới (hàng triệu lần trở lên), do đó chi phí của giải pháp ưu tiên đơn giản hơn, xấp xỉ bậc thấp hơn trong mỗi ô. Điều này đặc biệt đúng đối với các vấn đề ‘lưu lượng bên ngoài’, như luồng không khí xung quanh xe hơi hoặc máy bay, hoặc mô phỏng thời tiết.
Phần dịch về cơ sở toán học của Phương pháp phần tử hữu hạn (FEM) có nhiều chỗ chưa chính xác và gây hiểu nhầm. Mong các bạn cải thiện.