Lệnh cơ bản MATRIX 7 – Thiết kế nữ trang
Mục lục
1/ Menu Project trên phần mềm Matrix 7
1.1/ Những điểm mới
Projects trông hơi khác, đặc biệt vì các nút dùng để đóng toàn bộ menu nằm ở một vị trí tương tự như nút bấm sử dụng để mở rộng dòng công việc. Vì vậy, rất có thể bạn vô tình sẽ đóng menu Project một vài lần trước khi bạn làm quen với giao diện mới. Đừng lo lắng, bạn sẽ không mất nhiều thời gian để làm quen với những thay đổi này. Trong khi đó, nếu bạn vô tình đóng nó, chỉ cần nhấp F6 khi không chọn gì và chọn nút Project phía dưới cùng của menu để tải lại menu Project
Chúng tôi cũng di chuyển các nút để thêm một hàng dự án mới, tải một dự án hiện có và mở menu quản lý dự án ở dưới cùng của menu Project đối diện với đỉnh.
Hình ảnh mới của Projects bao gồm các tùy chọn nâng cao chứa Master Job Bags
Một số cải tiến khác để lưu ý là việc di dời Master job bags. Nó không còn nằm ở đầu menu, thay vào đó, sử dụng các tùy chọn nâng cao, nằm ở dưới cùng của menu Project để truy cập vào các túi công việc. Bạn cũng có thể chọn thêm Master job bags bằng cách nhấn vào dấu + nhỏ ở góc trên bên phải của mỗi túi các công việc. Khi bạn thêm một mục mới vào một túi công việc, trình tạo tự động chuyển tất cả các công việc vào túi bên trái, giúp bạn truy cập vào túi công việc tiếp theo.
Cần đề cập đến 1 mục nữa trước khi bỏ qua phần Project của giao diện trong Project Manager. Phần bổ sung mới “Turn Off All Job Bags” và “Turn On All Job Bags” cho phép bạn nhanh chóng chọn túi công việc để hiển thị trong menu Project. Nhấp vào các tùy chọn Turn Off All Job Bags, sau đó chọn Project Rows để hiển thị bằng cách chuyển đổi qua lại trên tùy chọn Select. Sau khi hoàn tất, chỉ cần đóng trình đơn Project Manager và xem những thay đổi này trong menu Project.
2/ Làm việc với chế độ mặt trên matrix 7
2.1/ Mặt
Khi chọn face mode, các mặt xác định bề mặt được chọn. Để chọn nhiều mặt, chọn và nhấn giữ phím Shift để nhóm nhiều mặt.
2.2/ Translate
Sử dụng mũi tên màu xanh dương, màu xanh lá cây và đỏ để giới hạn di chuyển trong một trục.
Sử dụng các đĩa màu xám để giới hạn sự chuyển động hai trục.
Hộp mòng két nằm ở trung tâm cho phép di chuyển tự do. Nó được sử dụng đặc biệt khi làm việc trong khung nhìn Perspective.
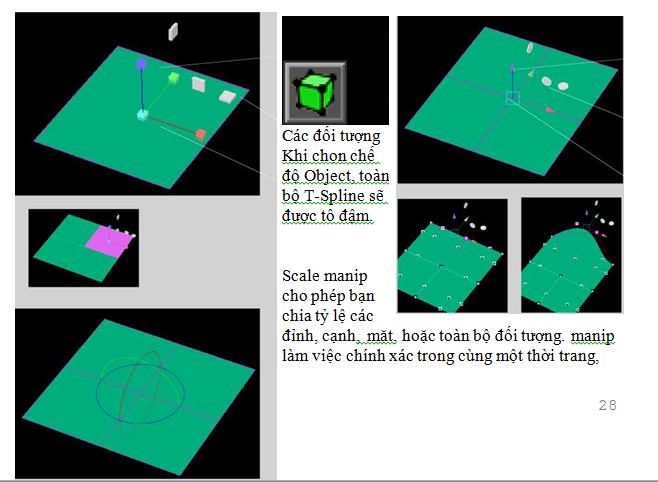
Các đối tượng khi chọn chế độ Object, toàn bộ T-Spline sẽ được tô đậm. Scale cho phép bạn chia tỷ lệ các đỉnh, cạnh, mặt, hoặc toàn bộ đối tượng, manip làm việc chính xác trong cùng một thời trang, tuy nhiên, về trực quan hơi khác một chút. Để mở rộng quy mô một mục theo 1 chiều, sử dụng các hộp màu xanh, đỏ, hoặc màu xanh lá cây. Để mở rộng quy mô một mục trong hai chiều, sử dụng những đĩa màu xám phẳng. Các đĩa được giới hạn trong mặt phẳng cụ thể, trong đó chúng được định hướng và cần được sử dụng để mở rộng quy mô cụ thể trong mặt phẳng. Để mở rộng quy mô các mục trong không gian ba chiều sử dụng hộp teal nằm ở trung tâm của manip.
2.3/ Scale
Sử dụng các hộp màu xanh dương, màu xanh lá cây và màu đỏ để mở rộng quy mô một mục trong một chiều.
Sử dụng các đĩa màu xám để quy mô mục theo hai chiều
Sử dụng hộp teal ở trung tâm của đối tượng để mở rộng các mục trong ba chiều.
2.4/ Rotate
Sử dụng các vòng tròn màu xanh dương, màu xanh lá cây và đỏ để xoay một mục xung quanh một trục.
2.5/ Tạo 1 mặt phẳng
Xác định lệnh T-Spline Plane từ trang thứ hai của trình đơn T-Spline của Matrix. Nhấp chuột vào lệnh Plane và chọn tùy chọn Center từ dòng lệnh. Địa điểm trung tâm của mặt phẳng ở F4. Nhập 10 trong dòng lệnh và nhấn Enter hai lần.
3/ Các công cụ tạo hình đá quý mới trong Matrix7
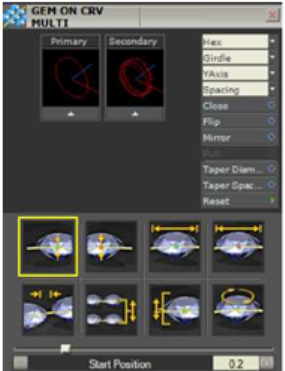
3.1/ Công cụ Gem on Curve
Cập nhật tính năng mới của công cụ Gem on Curve quyết định thêm nhiều công cụ thiết kế đá quý mới.
Trong khi xem công cụ Gem on Curve để thêm một vòng quay khác để xử lý chức năng của nó, nó đã được quyết định đi sâu vào công cụ này và xem những gì khác có thể được thực hiện. Trong khi làm như vậy, nhóm nghiên cứu phát triển Gemvision tạo ra một vài công cụ bổ sung: Gem on Curve Advanced, Gem Count on Curve, Gem List on Curve và Gem on Curve Multi.
Các công cụ mới này tiếp cận, thiết kế hình đá quý theo nhiều cách khác nhau. Vid thế, tùy thuộc vào kết quả của chúng ta tìm kiếm, chọn một công cụ khác cho 1 ứng dụng khác.
Gem on Curve được cập nhật với 2 tay quay bổ sung điều khiển tối đa với thiết kế đá quý.
4/ Độ tự do của các đường khi thiết kế
4.1/ Degree 1 Curve
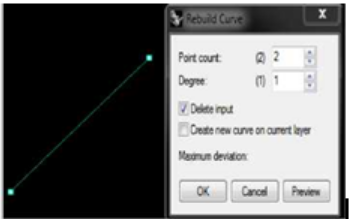
Single Line là ví dụ của Degree 1 Curve, Degree 1 Curve sẽ có các đường cong. Đó là 1 đường thẳng cứng sẽ mở rộng giữa 2 điểm trong khoảng cách.
4.1/ Degree 2 Curve
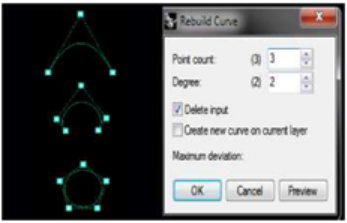
Degree 2 Curve có 1 đường cong, 1 số ví dụ của Degree 2 Curve là các đường parabolas, hyperbolas và đường cong.
4.3/ Degree 3 Curve
Degree 3 Curve có 2 đường cong. Khi thao tác bạn có thể sắp xếp điểm điều khiển để tạo mô hình zigzag H.U.D, BI
4.4/ T-Splines
Học cách thực hiện các chi tiết khác nhau của T-Splines bằng cách sử dụng các công cụ nằm trong màn hình hiển thị heads up.
T-Splines Head Up Display, hoặc H.U.D. là nút đầu tiên trong T-Splines Menu của Matrix. Khi nhấn, Head Up Display sẽ đọc ngay dưới Menu chính và chứa công cụ của bạn. Bạn có thể kéo và thả Menu này đến một vị trí mới có thể truy cập dễ dàng hơn, chẳng hạn như bất kỳ cửa sổ khung nhìn. Để làm như vậy, nhấp chuột vào thanh tiêu đề của H.U.D. và một vị trí mới.
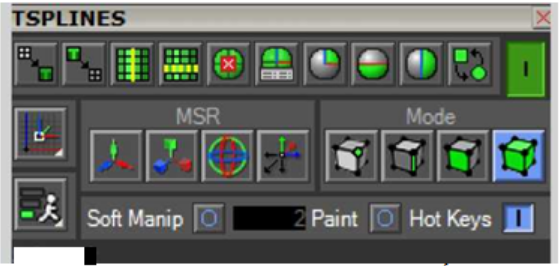
H.U.D. chứa nhiều công cụ hữu ích. Lưu ý rằng nút T-Splines On/Off ở góc phía trên bên phải. Nút này bị chuyển thành On để sử dụng công cụ T-Splines nằm trong H.U.D. Beginning ở góc phía trên bên trái và thực hiện qua Menu, các nút này như sau: Convert to T-Splines, Convert to Rhino Surface, Loop Select, Ring Select, Symmetry Off, Symmetry, X and Y Symmertry, Y Symmertry, X Symmertry, Box/Smooth Toggle, Drag Mode, MSR Translate (Move), Scale, Rotate, Set Pivot Point, Mode (Select Vert, Select Edge, Select Face, Select Object) và Speed Mode Menu. Đáy của H.U.D. chứa On/Off toggles; Sort Manipulation. Paint và Hot Keys cũng như feedback line “Selected”.
Hãy bắt đầu khám phá H.U.D. bằng cách vào deep end – hãy nói về các bề mặt converting Matrix cho T-Splines và ngược lại. Nó nằm ở tất cả Degree 1-3 stuff. Tại đây nó sẽ tập trung với lý do bạn cần biết lý thuyết sau bài toán của hình 3D.
5/ Gem List on Curve
Trình tạo này cũng được dựa trên công cụ Gem on Curve Advanced chứa tất cả chức năng của nó. Sự khác biệt khi sử dụng công cụ này là những viên đá quý bao gồm đá quý trên đường cong sẽ được xác định bởi một danh sách các đá quý mà bạn muốn trình tạo làm việc. Trình tạo này hoàn hảo khi làm việc với khách hàng đang sử dụng đá quý từ một mục đồ trang sức và biến chúng thành một cái gì đó mới. Cho phép bạn hạn chế các loại đá quý trong thiết kế đá quý trong danh sách. Trình tạo này cũng lý tưởng nếu bạn đang làm việc với đá quý bạn có trong kho và đang cố gắng để sử dụng nó.
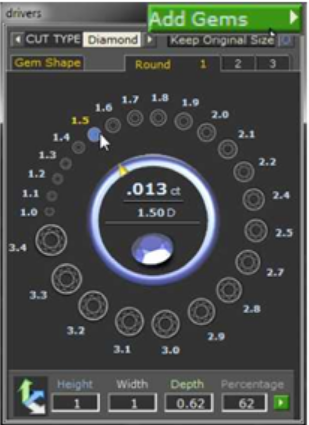
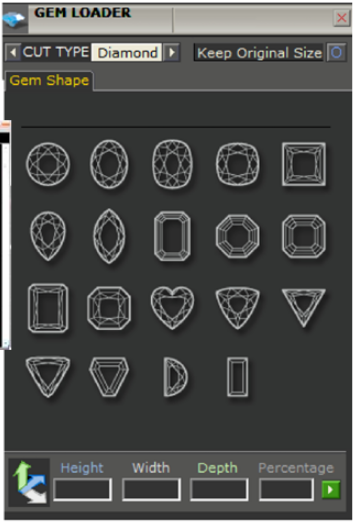
Bắt đầu bằng cách nhập một đường cong vào cửa sổ đường cong. Tiếp theo, xác định kích thước và hình dạng của đá quý bạn muốn sử dụng. Điều quan trọng là chọn những hình đá quý theo thứ tự bạn muốn chúng xuất hiện trong hàng đá quý. Sử dụng nút Add Gem để bắt đầu tạo danh sách đá quý. Làm như vậy sẽ mở menu Gem Loader.
Bạn có thể chọn hình đá quý và kích thước để thêm vào danh sách. Lặp lại tương tự để khi tất cả hình đá quý được thêm vào danh sách. Cập nhật danh sách sẽ xuất hiện trên đường cong và trong Gem List trên Curve Menu kế bên ô nhập liệu Curve. Đóng Gem Loader Menu. Nếu muốn sắp xếp lại thứ tự mà đá quý xuất hiện trong danh sách, sử dụng mũi tên lên xuống dưới danh sách đá quý. Tô đậm hình đá quý muốn thay đổi thứ tự và nhấn vào mũi tên phù hợp. Các thay đổi này sẽ tự động phản ánh trong khung xem. Nếu muốn xóa hình đá quý trong danh sách, hãy nhấn vào nó và sử dụng nút X nằm dưới danh sách.
Các thay đổi đối với danh sách hình đá quý được phản ánh trong khung nhìn.
Các công cụ còn lại trong Menu này được tiêu chuẩn hóa qua tất cả các công cụ Gem on Curve.
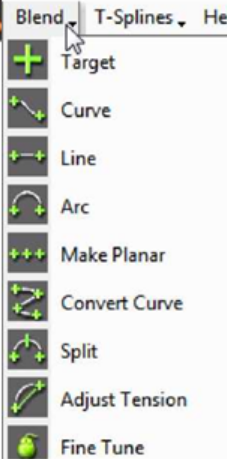
6/ Blend và VS. T-Splines
Trong Matrix menu, bạn sẽ thấy rằng T-Splines menu nằm tại vị trí của Targets menu trước đây. Bạn có thể truy cập vào tất cả công cụ Blend Targets trong Blend menu trên đỉnh giao diện.
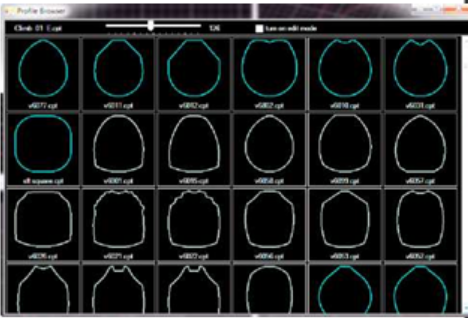
6.1/ Profile Browser
Profile Browser vẫn chứa các chức năng tương tự. Sử dụng thanh trượt ở trên cùng của menu để thay đổi quy mô của các hình ảnh thu nhỏ. “turn on edit mode” cho phép bạn thay đổi thứ tự của tiết diện. Hãy nhớ chuyển nút này ‘Off’ để rời menu này để thực hiện những thay đổi. Nhấp chuột phải vào bất kỳ cấu hình nào để chỉnh sửa các lớp màu trong tiết diện.
Những người lập trình Gemvision đã làm việc để tùy chỉnh trình tạo này để tất cả Profile Browsers này tải nhanh hơn, giúp tiết kiệm thời gian và kiếm được nhiều tiền hơn. Hơn nữa, các trình duyệt tải nhanh hơn, thư viện Outside Ring Rail Library được cung cấp makeover. Mỗi Rail được vẽ lại để thân thiện hơn với người dùng và làm việc trơn tru với 1 số trình tạo trong chương trình.
6.2/ Gem Loader
Gem Loader Menu có hình ảnh mới phù hợp hơn với người dùng. Một số hình đá quý được thay đổi và dựa vào hình 3D. Các sản phẩm này có thông tin chính xác về hình đá quý cũng như có chất lượng render tốt hơn. Gem Loaded mới cũng chứa 1 hình đá quý mới. Square Cushion.
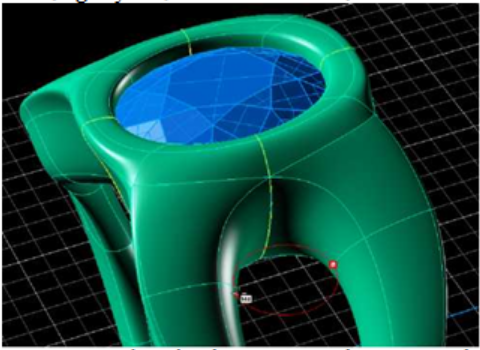
7/ Tạo T-Splines Signet Ring
7.1/ Cách thực hiện
Click nút + Ring Rail và chọn kích thước chiếc nhẫn. Click dấu mũi tên màu xanh để đặt vành nhẫn trong khung nhìn.
Từ menu trình tạo Signet, nhấn nút Start.
Trong cổng nhìn. Khởi động Signet Builder bằng cách nhấn nút Start. 1 chiếc nhẫn T-Spline signet sẽ xuất hiện trên màn hình với khung nhìn điều khiển tay quay được sử dụng để tạo thay đổi cho thiết kế. Sử dụng thành trượt trên trình tạo T-Splines Signet hoặc tay quay điều khiển khung nhìn để thay đổi bản thiết kế. Nhấn nút Enter để kết thúc lệnh. History không được kích hoạt trên công cụ này sau đó kết thúc lệnh, bạn có thể truy cập vào tay quay điều khiển khung nhìn để tạo điều chỉnh. Tuy nhiên, sử dụng nút Start để khởi động lệnh lần nữa và trình tạo này sẽ tự động bắt đầu với các thiết lập cuối cùng được sử dụng
8/ Tạo bề mặt TS Signet và Bezels
8.1/ Nguyên nhân
T-Splines Signet và Bezel được tạo ra để giúp bạn bắt đầu với đối tượng T-Spline đơn giản có thể dễ dàng thao tác và tạo đồ trang sức đẹp. T-Splines Signet và T-Splines bezels là các lệnh Matrix cụ thể sẽ không được tìm thấy nếu bạn đang chạy T-Splines ngoài Matrix.
8.2/ T-Splines Signet
Lệnh T-Splines Signet nằm ở trang thứ 2 của Matrix’s T-Splines menu. Bắt đầu lệnh và menu trình tạo Signet nằm dưới.
Bắt đầu bằng cách đặt một vành đai nhẫn trên màn hình. Để làm điều này, nhấn vào nút + Ring Rail và menu Set Ring Rail sẽ xuất hiện. Sử dụng trình đơn thả xuống để chọn kích
Sử dụng hoặc xử lý kiểm soát khung nhìn hoặc các thanh trượt trong menu để thay đổi Signet. Sau khi làm xong bấm Enter để kết thúc lệnh. Hãy nhớ, bạn có thể tiếp tục thay đổi các Signet bằng cách sử dụng lệnh T-Splines tiêu chuẩn
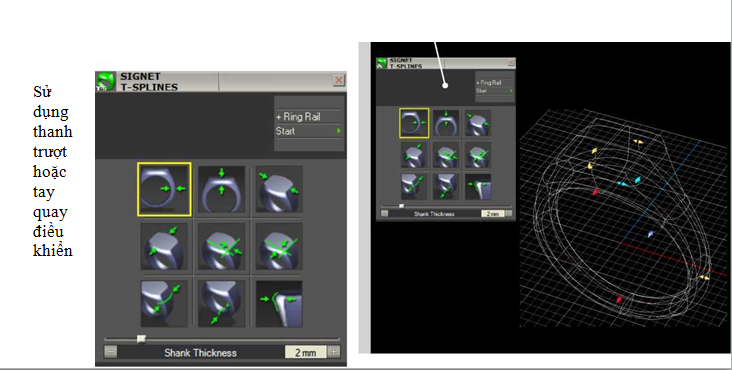
Sử dụng thanh trượt hoặc tay quay điều khiển khung nhìn để điều khiển kích thước nhẫn và nhấn vào mũi tên màu xanh lá cây để đặt vành chiếc nhẫn. Click Enter.
Nằm trên trang thứ 2 của T-Splines menu của Matrix, click vào trình tạo T-Splines Signet .
9/ Các hình khối T-Splines
9.1/ Lệnh Plane
Lệnh Plane vẽ gốc mặt phẳng hình chữ nhật hoặc hình vuông T-. sự khác nhau duy nhất trong tùy chọn dòng lệnh giữa mặt phẳng và hộp là mặt phẳng không có tùy chọn để thêm mặt theo trục Z. điều này giúp xem xét mặt phẳng có chiều dài và chiều rộng nhưng không có chiều cao.
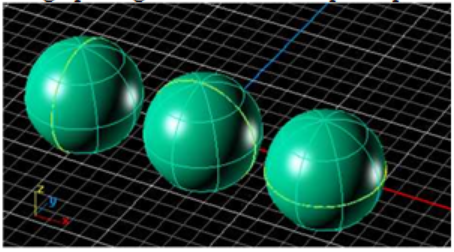
9.2/ T-Spline Sphere
Lệnh T-Splines Sphere cũng rất đơn giản để sử dụng.
Bắt đầu lệnh và theo gợi ý “Center of sphere”. Click vào bất cứ đâu trong khung nhìn để bắt đầu vẽ hình cầu. Giống như lệnh Box, bạn có thể nhập giá trị kích thước hình cầu hoặc xác định kích thước hình cầu bằng mắt. hình cầu xuất hiện và và dòng lệnh đưa ra các tùy chọn bổ sung: “Smooth”, “Vertical Faces”, “Around Faces” và “Symmetry”. Các tùy chọn này làm việc như lệnh Box. Tùy chọn “Smooth” cho phép bạn chuyển đổi giữa chế độ Smooth và Box Mode. Các tùy chọn “Vertical Faces” và “AroundFaces” cho phép bạn đọc giá trị số mặt bạn muốn thêm vào theo 2 hướng. “Vertical Face” giống như kinh độ và “Around Face” giống như vĩ độ của địa cầu. Nếu tùy chọn “Symmetry” chuyển thành “Yes” , các tùy chọn cho “Axial” và “Radial Symmetry” xuất hiện. Kết quả là tùy chọn Axial symmetry chuyển thành “No”. ngay khi chuyển tùy chọn này thành “Yes” tùy chọn dòng lệnh mở rộng
Để chứa “X-Symmetry”, “Y-Symmetry” và “Z-Symmetry”.
Khi điều khiển một quả cầu đã được tạo ra với đối xứng trục bật lên thành “Yes” trên bất kỳ trục nào, kết quả trong một đối tượng là như nhau ở cả hai bên. Nói cách khác, nó giống như đặt một tấm gương dọc theo trục. Khi mục được thao tác, bạn sẽ thấy những thay đổi nhân đôi dọc theo trục được lựa chọn. Theo mặc định, “Radial Symmetry” được bật lên thành “No”. Ngay sau khi bạn chuyển đổi tùy chọn này thành “Yes”, các tùy chọn “SymmetrySegments” và “FacesPerSegment” sẽ có sẵn. Đối xứng xuyên tâm được xác định từ tâm của các đối tượng ra ngoài trái ngược với trục của nó. Tùy chọn “SymmetrySegments” cho phép bạn xác định có bao nhiêu dòng đối xứng để phân chia các quả cầu . Sự phân chia này xảy ra giống như cắt một chiếc bánh thành các phần. Giá trị bạn xác định sẽ quyết định có bao nhiêu miếng bánh bạn sẽ cắt thành hình cầu. hình cầu sẽ xuất hiện với các đường thẳng màu cam cho thấy các đường đối xứng. Chỉ báo trực quan này sẽ vẫn còn trên hình cầu cho đến khi đối xứng được lấy ra từ các đối tượng.
Tùy chọn “FacesPerSegment” xác định có bao nhiêu mặt sẽ được thêm vào xuyên tâm cho mỗi dòng đối xứng. Các lệnh T-Splines Sphere có các tùy chọn dòng lệnh bổ sung.
Màn hình, các điểm sẽ chạm vào hình cầu. Với hơn 3 điểm, chương trình sẽ tạo khoảng cách trung bình giữa chúng để tạo hình tròn.
T-Splines Sphere không có nhược điểm. Thực hành tốt nhất khi tạo các đối tượng T-Spline là tạo mặt với chính xác bốn cạnh. Điều này không phải là để nói rằng một mặt ba chiều không thể chấp nhận, chỉ là nếu bạn đang nhập các đối tượng này vào một chương trình phần mềm, các chương trình khác không thể nhận ra các bề mặt này. Không có mặt 4 chiều nào có thể tạo ra star-points, n-gons và t-points. Chúng tôi sẽ thảo luận về các chi tiết cụ thể của T-Spline thiết kế sau này trong hướng dẫn. Một lần nữa, điều này hoàn toàn chấp nhận được trong T-Splines và Matrix, nhưng nếu bạn làm việc với phần mềm khác, mà bạn muốn tạo hình dáng đơn giản bằng cách sử dụng lệnh QuadBall sử dụng 4 mặt.
Lệnh Quadball tạo hình cầu, tuy nhiên đối tượng được tạo với 4 mặt. Các tùy chọn QuadBall là các tùy chọn tương tự như T-Splines Sphere.
9.3/ Axial Symmetry
Hình cầu bên trái có đối xứng trục áp dụng trong các trục X. Hộp ở giữa có trục đối xứng áp dụng ở trên trục Y. Hộp bên phải có đối xứng trục áp dụng ở trên trục Z
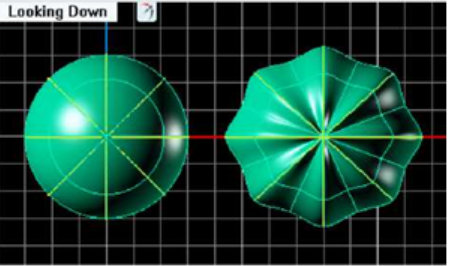
9.4/ Radial Symmetry
Radial Symmetry phân chia các đối tượng như cắt một chiếc bánh. Ảnh dưới đây tùy chọn đối xứng được thiết lập thành 8, đặt 8 dòng đối xứng xung quanh hình cầu. Bên phải, thay đổi được thực hiện cho một trong những phân đoạn và phần còn lại của phân khúc phản ánh những thay đổi này.
Tùy chọn “2Point” để vẽ hình cầu từ cuối đường kính này đến đường kính khác, tùy chọn “3Point” thể hiện 3 điểm mà quả cầu đi qua và lệnh “Tangent” được sử dụng để tạo hình cầu tiếp xúc với 1, 2 hoặc 3 đường cong hoặc bề mặt. Click vào 1 đường cong để bắt đầu, sau đó chọn 1 điểm trên 1 đối tượng. Điều này giúp thay đổi đến khi điểm thứ 3 được đặt. “Point” sẽ được chọn 1 điểm, không phải 1 đường cong hoặc bề mặt.
Sử dụng tùy chọn “FitPoint” để tạo hình cầu từ 3 hoặc nhiều điểm.
Khi bạn muốn bắt đầu một quả cầu từ một đầu của nó có đường kính và kết thúc ở đầu kia và cho ví dụ, hình cầu cần phải chạm vào hai đối tượng, sử dụng tùy chọn “2-Point” cùng với O-Snaps. Tương tự như vậy, nếu bnaj cần các hình cầu chạm vào ba điểm trong không gian, sử dụng tùy chọn “3-Point”.
10/ Đối xứng trục-Axial Symmetry
10.1/ Box & Axial Symmetry
Click lệnh tsBox. Trong dòng lệnh, bật tùy chọn ” AxialSymmetry” là “Yes”. Dòng lệnh sẽ mở rộng ra, thêm các tùy chọn mới cho hình đối xứng theo trục X, Y, Z. Chọn 1 hoặc nhiều hình đối xứng.
Tạo thay đổi cho đối tượng sẽ tự động đối xứng thay đổi này theo trục đối xứng.
Nhấn vào trong khung nhìn để chọn góc đầu tiên của hộp. Các cú nhấp chuột tiếp theo xác định chiều dài và chiều rộng. Thay đổi khung nhìn để xác định chiều cao. Nhấn để kết thúc lệnh.
Thao tác với phép đối xứng:
Dòng ở giữa hộp dọc theo trục giao tiếp mà đối xứng được áp dụng. Tạo thay đổi ở 1 cạnh của hộp sẽ tự động phản ánh sự thay đổi này trên trục đối xứng, trong đó được áp dụng.
11/ Các chế độ tạo Gốc
11.1/ Công dụng
Sử dụng hình dạng gốc để bắt đầu thiết kế trong T-Splines là một cách rất đơn giản và dễ dàng để bắt đầu – và là một cách tuyệt vời để làm quen với các công cụ và MSR Mode trong HUD.
Các gốc bao gồm hộp, mặt phẳng, cầu, Quadball, xi lanh, hình nón và xuyến. Hầu hết các kiểu gốc là đối tượng đóng – với ngoại lệ là các công cụ xi lanh. Gốc có thể được sử dụng như các đối tượng riêng và / hoặc chúng có thể được kết hợp với các đối tượng T-Spline khác để tạo ra mô hình phức tạp.
Khi tạo gốc, điều quan trọng là phải quan sát dòng lệnh. Có nhiều tính năng có sẵn ở đây được sử dụng để xác định số lượng và loại điều khiển, bạn sẽ có trong đối tượng.
Nhiều đối tượng gốc có các tùy chọn Command line chung với nhau. Ví dụ, lệnh T-Splines Box cũng tương tự như T-Splines lệnh Plane, vì vậy hãy tham khảo phần ô hướng dẫn để biết chi tiết về các tùy chọn Command line .
11.2/ T-Splines Box
Hãy bắt đầu bằng cách khám phá lệnh Box. Bắt đầu lệnh Box và thực hiện theo các nhắc nhở dòng lệnh . Dấu nhắc đầu tiên sẽ đọc “góc đầu tiên của cơ sở”. Nhấn vào bất cứ nơi nào trong khung nhìn Looking Down để bắt đầu vẽ một Box T-Spline. Dấu nhắc tiếp theo sẽ là “góc cơ sở khác hoặc chiều dài”, click chuột này sẽ xác định chiều dài và chiều rộng của hộp. Nếu bạn biết kích thước chính xác cho hộp, bạn có thể nhập các tùy chọn T-Splines Box Command Line
11.3/ Các tùy chọn
Hãy cùng khám phá các tùy chọn dòng lệnh. Đầu tiên, xóa hộp khỏi màn hình. Để làm điều này, kích hoạt chế độ Object và nhấp vào hộp để chọn nó, sau đó nhấn nút Delete trên bàn phím.
Bạn có thể nhận thấy rằng hộp cuối cùng đã được tạo ra có 1 số mặt theo cụ thể theo từng trục. Theo mặc định, giá trị này được thiết lập là 2 trong trục X, Y và Z. Thật dễ dàng, tuy nhiên, để thay đổi những giá trị này và thêm mặt vào hộp trong quá trình tạo nó. Bắt đầu lệnh Box và lưu ý các tùy chọn dòng lệnh “Xfaces = 2, Yfaces = 2 và Zfaces = 2”. Nhấp vào bất kỳ tùy chọn nào trong dòng lệnh và nhập một giá trị số vào dòng lệnh để xác định thiết lập mặt của hộp trong một trong ba trục.
Các tùy chọn dòng lệnh bổ sung cho phép bạn để khởi động Box tại tâm hoặc đặt nó làm tâm trên một đối tượng khác nếu Center O-Snap được bật.
11.3.1/ Center
Tùy chọn dòng lệnh “Center” bắt đầu vẽ hộp từ tâm ra ngoài.
Các dòng lệnh sẽ hiển thị dấu nhắc “Chiều cao”. Nhấn Enter để sử dụng “Width”. Nếu bạn muốn chiều cao phù hợp với chiều rộng chính xác, nhấn Enter. Nếu không, thay đổi khung nhìn Through Finger và kéo con trỏ tới chiều cao mong muốn cho T-Spline Box. Trong khi ở giữa lệnh, mục sẽ xuất hiện như một loạt các đường thẳng biên dạng hình dạng bên ngoài và hình dạng trở nên cứng ngắc. Các đối tượng kết quả sẽ mềm mại hơn như một miếng kẹo gum Hubba Bubba. T-Spline Box của bạn đã sẵn sàng để được thao tác. Chọn chế độ thích hợp (Vert, Edge, Face hoặc Object) và công cụ MRS để bắt đầu chỉnh sửa và xác định hình dạng hộp.
11.3.2/ Vertical
Tùy chọn Vertical cho phép bạn chọn chiều dài, chiều rộng và chiều cao của hình chữ nhật và cũng cho phép bạn vẽ hộp ở một góc.
11.3.3/ Smooth
Tùy chọn “Smooth” chuyển đổi giữa “Yes” và “No” và xác định các đối tượng được tạo ra trong chế độ Smooth Mode hoặc Box Mode.
11.3.4/ 3Point
Tùy chọn “3Point” cho phép bạn dễ dàng rút ra hộp trên 1 góc.
11.3.5/ Axial Symmetry
Các tùy chọn dòng lệnh cuối cùng chúng ta sẽ nói đến là tùy chọn “Axial Symmetry”. Theo mặc định, tùy chọn này được bật lên thành “No”. Ngay sau khi bạn chuyển đổi tùy chọn này thành “Yes”, các tùy chọn dòng lệnh mở rộng để bao gồm “X-Symmetry”, “Y-Symmetry”, “Z-Symmetry”. Khi thao tác với một hộp thoại
12/ MSR và Mode
12.1/ Cách sử dụng
Click lệnh T-Splines H.U.D. để mở Heads Up Display.
Chọn công cụ Scale và chế độ đối Object.
Click vào máy bay.
Chia tỷ lệ các mục bằng cách sử dụng đĩa màu xám trên mặt phẳng XY. Lưu ý mặt phẳng được thu nhỏ từ tâm của đối tượng.
12.2/ Rotate manip
Rotate manip cho phép bạn xoay đỉnh, cạnh, mặt, hoặc toàn bộ đối tượng. Rotate manip rất đơn giản để sử dụng. Khi hoạt động, một tập hợp các vòng tròn màu đỏ, xanh lá cây và màu xanh dương bao quanh đối tượng. Mỗi vòng tròn xác định các trục sẽ diễn ra luân chuyển .
Theo mặc định, mỗi thao tác được đặt ở trung tâm của đỉnh, cạnh, mặt hoặc toàn bộ đối tượng đang được chế tác. Nói cách khác, nếu bạn tạo ra một hộp ranh giới xung quanh đối tượng và đặt một điểm ở trung tâm, đây là nơi mà manip sẽ xuất hiện khi bắt đầu.
12.3/ Lệnh Set Pivot Pivot
12.3.1/ Công dụng
Lệnh Set Pivot Pivot cho phép bạn thay đổi vị trí của manip, cho phép bạn tiếp tục kiểm soát cách thay đổi các đối tượng .
Thay đổi điểm quay
12.3.2/ Cách dùng lệnh Set Pivot Pivot
Click biểu tượng Set Pivot Point từ H.U.D.
Dòng lệnh sẽ nhắc nhở “chọn điểm”. thay đổi vị trí chia tỷ lệ bằng cách nhấn vào mặt phẳng ở góc phía dưới bên trái.
Chia tỷ lệ mục bằng cách sử dụng đĩa màu xám trong mặt phẳng XY để so sánh.
13/ Smart Flow AutoBase
13.1/ Chức năng
Trong phiên bản trước, bạn đã có để tạo ra bề mặt phẳng từ bề mặt 3D bằng cách sử dụng Create UV curve. Và từ những đường cong, bạn được yêu cầu để tạo ra một bề mặt. Các tính năng mới trong lệnh Smart Flow làm tất cả điều này cho bạn.
13.2/ Cách sử dụng
Có hai cách khác nhau để sử dụng chức năng này:
+ Cách 1:
- Một cách để truy cập chức năng Autobase là để làm nổi bật các mô hình 3-D trước khi chạy lệnh Smart Flow. Sau khi làm như vậy, tùy chọn Command line option AutoBase xuất hiện. Nhấn vào tùy chọn này và một mặt phẳng hoặc Autobase sẽ xuất hiện xác định mô hình 3-D. Đặt ra một mô hình về Autobase này và mô hình sẽ tự động cập nhật với bề mặt 3-D.
+ Cách 2:
- Sử dụng nút SmartFlow AutoBase. Với đối tượng 3-D trong khung nhìn, chạy lệnh SmartFlow Autobase
- Click nút Smart Flow AutoBase. Mặt phẳng sẽ tự động được tạo.
- Click nút Smart Flow và tạo mối quan hệ giữa Base surface và Destination surface, các mục trong bề mặt sẽ không chạy.
- Mặt phẳng sẽ xuất hiện và bất kỳ mục nào trong bề mặt sẽ tự động chạy xuống bề mặt đích.

Ví dụ sử dụng Smart Flow AutoBase
Các dòng lệnh sẽ nhắc nhở, “Chọn địa điểm để tạo autobase”. Chọn mô hình 3-D,, chức năng này chỉ hoạt động trên 1 bề mặt duy nhất.
Nếu mô hình của bạn bao gồm nhiều bề mặt, điều này có thể có vấn đề vì chỉ có phần riêng của polysurface được click vào sau dấu nhắc để “Chọn địa điểm để xây dựng autobase” sẽ tạo ra các bề mặt phẳng để thiết kế. Sau khi tạo auto base bằng cách sử dụng tính năng Smart Flow Autobase, bạn vẫn phải chạy lệnh Smart Flow và làm theo các hướng dẫn để chọn Base Surface Object (bề mặt phẳng), và Select the Destination Surface Object” (3-D model). Các mẫu nằm trên autobase sẽ tự động tịnh tiến vào bề mặt đích.
14/ Tạo T-Splines Bezel
14.1/ Chỉnh sửa Bezel
Sử dụng thanh trượt trong Menu hoặc xử lý khung nhìn để thay đổi bezel. Các lệnh T-Splines Bezel và Under Bezel tạo T-Spline bezel/under bezel chỉnh sửa quanh nhiều hình đá quý của Matrix.
14.2/ Cách làm
- Đặt hình đá quý tròn trên khung nhìn
- Khởi động lệnh T-Splines Bezel và Bezel T-Splines menu.
- Đánh dấu viên đá quý và nhấp vào mũi tên đi lên để đặt các viên ngọc vào cửa sổ Gem trong menu. Một bản xem trước của bezel T-Spline sẽ xuất hiện cùng với một loạt các xử lý kiểm soát khung nhìn có thể được sử dụng để thay đổi kích thước của bezel. Tất cả các xử lý kiểm soát khung nhìn có liên quan đến một trong những điều khiển trượt nằm trong menu T-Splines Bezel.
- Sử dụng một trong hai phương pháp để thay đổi bezel.
Ngoài việc kiểm soát các kích thước bezel, bạn cũng có thể bật tắt điều khiển cho dù một số phần của bezel có nếp nhăn cạnh. Những khu vực này bao gồm phần trên của bezel, chỗ ngồi của bezel và các cơ sở của bezel. Vì vậy, tùy thuộc vào ứng dụng, bạn có thể quyết định để chuyển đổi một số các tùy chọn này vào vị trí ‘On’ để thêm mép cứng vào vùng mô hình.
Nằm Nằm dưới On / Off Toggles là một chuyển đổi cho phép lựa chọn các tùy chọn “ít” và “nhiều”. Thiết lập này xác định có bao nhiêu cạnh được sử dụng để tạo ra các hình dạng tổng thể của bezel.
Sau khi hoàn thành tất cả các thay đổi mong muốn sử dụng các tùy chọn tìm thấy trong menu và xử lý kiểm soát khung nhìn, nhấp Enter. Điều này sẽ kết thúc lệnh và bezel hoàn tất sẽ xuất hiện trong khung nhìn. Sau khi làm như vậy, bạn có thể tiếp tục chỉnh sửa bezel bằng cách sử dụng thao tác T-Splines, nhưng bạn không thể truy cập các xử lý kiểm soát khung nhìn. Vì vậy, hãy chắc chắn bạn hoàn toàn được thực hiện với những thay đổi của bạn trước khi kết thúc lệnh.
15/ Chức năng F6 mới
15.1/ Chức năng
Menu phím tắt F6 được mở rộng để chứa nhiều công việc cụ thể mà bạn thực hiện.
F6 được thiết kế để ngay lập tức cung cấp một danh sách các liên kết đến các chức năng và các công cụ liên quan đến đối tượng được chọn, Menu ngữ cảnh này đã trở thành một công cụ highly sử dụng phím tắt từ việc phát hành Matrix với Matrix 7, công cụ F6 bây giờ đã được mở rộng. Không chỉ có thể truy cập tùy chọn cơ bản như trước đây mà còn là một mảng rộng lớn hơn của tổ chức chặt chẽ, các lựa chọn được phân loại cũng có sẵn. Bấm vào tùy chọn đầu tiên Mode Select và chọn một trong năm hướng khác nhau.
Tùy thuộc vào loại bạn chọn, một danh sách mới của các công cụ liên quan sẽ xuất hiện.
15.2/ Các chế độ
Nó trực quan hơn bao giờ hết. Năm chế độ khác nhau bao gồm:
- Genaral Modeling
- Curve Layout
- Gem Layout
- Surface Modeling
- T-Spline Modeling
Mỗi chế độ có chứa một tập hợp khác nhau của các công cụ bên trong. Phương pháp tiếp cận F6 menu mới này nằm trong 1 context menu dễ dàng tiếp cận với công cụ bạn cần tìm kiếm nhanh hơn và hiệu quả hơn. Sau khi chọn một chế độ trong F6, lần sử dụng tiếp theo sẽ tự động bắt đầu trong chế độ đã được sử dụng.
Nếu bạn muốn thay đổi chế độ, chỉ cần nhấp Mode Select .
15.3/ Tùy chỉnh phím F6
Nằm ở đáy cửa sổ Modes Menu là tùy chọn Customize Menu. Nó mở Object Actions Editor. Được liệt kê trong bộ chỉnh sửa là tất cả các chức năng hiển thị cho chế độ mới trong F6.
Ở góc trái bên trên, click nút Add. 1 hàng mới được thêm vào sơ đồ và cột Name and Command sẽ độc ‘New Line’. Cả 2 miền này đều có thể chỉnh sửa. Chỉ cần nhấn và ‘swipe’ tên. Nó sẽ tô đậm Customizing F6
B1: Đầu tiên, xác định danh sách menu mà bạn muốn chỉnh sửa. đó có phải là General Modeling list cho Curves không? Nếu vậy, click vào đường cong và nhấn F6.
B2: Click Mode Select sau đó chọn General Modeling. Ở đáy danh sách, bạn sẽ thấy Customize Menu. Click vào nó. Nó sẽ mở This Object Action Editor.
B3: Để đặt 1 lệnh mới vào danh sách Modes F6 cụ thể này, click lệnh Add. NewLine sẽ xuất hiện với chữ này trong cột Name và Command. Đổi tên cột. Cách dễ nhất để xác định chính xác chữ được đặt trong cột Command để chạy lệnh trong Matrix.
B4: Sau khi chạy lệnh, dòng phản hồi trên dòng Command hiển thị chính xác chữ bạn cần nhập vào cột Command, nhưng loại bỏ nét gạch xuất hiện trước chữ. Trong hình dưới, lệnh _Fillet được nhập vào cột command là Fillet.
15.4/ Định vị lại thứ tự hàng trong danh sách
Định vị lại thứ tự hàng trong danh sách bằng cách sử dụng tùy chọn Move Down. Color code tạo mã lệnh này trong danh sách bằng cách thêm 1 quả cầu trước lệnh.
B1: Click trong cột nhỏ trước cột Name và 1 dấu mũi tên nhỏ xuất hiện. Sử dụng dấu mũi tên để định vị màu phù hợp từ danh sách.
B2: Khi đã hài lòng, click Save.Màu xanh và bạn có thể nhập lại tên chức năng cũng như lệnh. Để thêm chức năng chính xác, bạn cần biết tên lệnh chương trình tương đương cần để kích hoạt công cụ.
15.5/ Định vị tên lệnh chương trình
Để định vị tên lệnh chương trình liên quan đến chức năng bạn thêm vào, bạn cần khởi động công cụ này trong Matrix.
Ví dụ, nếu thêm chức năng Sweep 1 vào danh sách, bạn có thể xác định tên lệnh bằng cách nhấn vào đường cong, sau đó nhấn Sweep 1.
Chọn thứ tự của lệnh bằng cách sử dụng tùy chọn Move Up và Move down. Nếu muốn thêm quả cầu màu trước tên, click vào cột và hàng tương đương và mũi tên lên xuống sẽ xuất hiện. Chuyển đổi giữa các tùy chọn này đến khi tìm thấy quả cầu có màu phù hợp. Khi hoàn tất, nhấn nút Save.
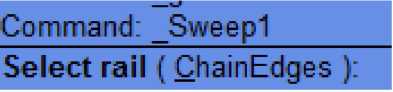
Chức năng Sweep 1
Vùng Line feedback. Có lệnh tương đương. Thông tin lệnh này được sao chép vào miền Object Action Editor ‘Command’. Chỉ nhập chữ/số cho lệnh.
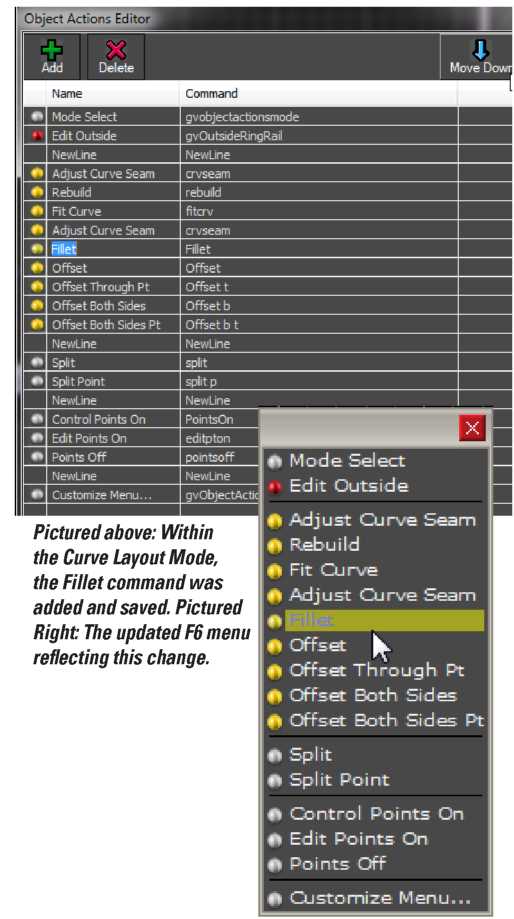
Hộp thoại Object Actions Editor
16/ Chuyển đổi từ T-Spline thành Matrix
16.1/ Chuyển đổi
Chuyển đổi T-Spline thành bề mặt nurbs là tất cả T-Splines tương thích 100% với nurbs, giúp T-Splines độc đáo và mạnh mẽ. Vào T-Splines bằng cách tạo ra mô hình siêu phức tạp, sau đó nhấp vào nút ‘Convert to Matrix’ và xem kết quả. Bạn sẽ ngạc nhiên rằng T-Splines sẽ chuyển đổi mô hình của bạn trở lại thành NURBS.
Trước khi chuyển đổi mô hình T-Splines thành NURBS, hãy chắc chắn là đã chuyển đổi Speed Mode thành Compatibility.
16.2/ Các bề mặt đơn sẽ được chuyển đổi
- Polysurfaces sẽ không được chuyển đổi.
- T-Splines sẽ ghi nhớ tất cả thông tin trim trong khi chuyển đổi.
- Tất cả đổi tượng Matrix được tạo ra với các cạnh thẳng.
16.3/ Chọn chế độ
Mép
Khi Edge mode được kích hoạt, 1 hoặc nhiều mép sẽ xác định bề mặt được chọn. Để chọn vòng lặp của mép, click vào 1 mép để nhấn mạnh nó sau đó nhấp đúp chuột để chọn vùng lặp mép
Đỉnh
Khi chế độ Verts được chọn, 1 đỉnh (điểm xác định) bề mặt có thể được chọn. Để chọn nhiều điểm, chọn và nhấn giữ phím Shift để lấy nhiều đỉnh
Chọn Mode và MSR
Khi bạn bỏ qua H.U.D.1 lát bởi vì các nút sẽ có ý nghĩa nếu chúng ta xem Mode and MSR của H.U.D. T-Spline Object chứa các đỉnh (điểm), mép và mặt (bề mặt). Trong phần Mode của H.U.D chứa các nút cho đỉnh, cạnh, mặt và các đối tượng
Chức năng của MRS
Các khối tạo cơ bản trên 1 đối tượng T-Spline mà thay đổi mỗi mục bằng cách sử dụng trên màn hình; Move, Scale và Rotate. Ngoài những chức năng chính, MSR cũng chứa các lệnh Set Pivot Point làm việc cùng với Move, Scale hoặc Rotate – cho phép bạn chọn vị trí mà bạn muốn di chuyển, đo đạc hoặc quay.
MSR và Mode làm việc kết hợp
MSR và Mode làm việc kết hợp với nhau:
- Trước tiên, bạn phải quyết định đối tượng bạn muốn thực hiện; một đỉnh (hay một nhóm các đỉnh), cạnh, mặt hoặc toàn bộ đối tượng T-Spline.
- Chọn loại đối tượng bạn muốn thao tác từ phần Mode của HUD.
- Khi được chọn, chế độ mà bạn đang làm việc sẽ có màu xanh dương.
- Tiếp theo, khi muốn thao tác các đối tượng trong phần MSR của HUD. Một lần nữa, tùy chọn MSR hoạt động sẽ có màu xanh dương.
Move (Translate) manipulator cho phép bạn di chuyển đỉnh, cạnh, mặt, hoặc toàn bộ đối tượng. Manip bao gồm mũi tên màu đỏ, xanh dương và xanh lá cây , các đĩa nhỏ màu xám và một hình vuông mòng két nằm ở trung tâm của manip. Các mũi tên màu cho phép bạn di chuyển các đối tượng cùng một trục. Các đĩa màu xám cho phép tự do hơn trong di chuyển và cho phép bạn di chuyển các mục trong hai mặt phẳng. Sử dụng hình vuông mòng két cho phép bạn di chuyển mục bất cứ nơi nào trong không gian ba chiều. Điều này đặc biệt hữu ích khi bạn đang làm việc trong khung nhìn Perspective.
17/ Chuyển từ Matrix thành T-Spline
2 nút đầu tiên trong T-Splines H.U.D. được sử dụng để chuyển đổi các mục trong và ngoài T-Splines. Trước tiên, bạn phải hiểu những gì các loại bề mặt tương thích với T-Splines. Một polysurface sẽ không chuyển đổi sang một T-Spline. Để chuyển đổi một polysurface từ Matrix thành T-Splines, các polysurface phải lần đầu tiên chuyển đổi và mỗi bề mặt sẽ cần phải được chuyển đổi.
17.1/ Các công cụ nằm trong Heads Up Display
Các công cụ nằm trong Heads Up Display được liệt kê từ trái sang phải:
- Convert to T-Splines
- Convert to Rhino Surface
- Loop Select, Ring Select
- Symmetry Off
- Symmetry X and Y Symmetry, Y Symmetry, X Symmetry
- Box/Smooth Toggle
- Drag Mode
- MSR (Translate (Move)
- Scale
- Rotate
- Set Pivot Point)
- Mode (Select Vert, Select Edge, Select Face, Select Object)
- Speed Mode menu.
Các công cụ MSR và các công cụ Mode làm việc cùng với nhau.
Đầu tiên, chọn chế độ bạn muốn làm việc với hoặc một phần của mô hình mà bạn muốn thao tác. Tiếp theo, chọn công cụ MSR hoặc cách bạn muốn thao tác Mode.
Đáy của T-Splines H.U.D. chứa On / Off. Thay đổi các thiết lập này sẽ thay đổi T-Splines hiệu suất tổng thể. Với ngoại lệ của các phím nóng chuyển đổi, các điều khiển khác trong menu này để thiết lập lại vị trí mặc định của họ mỗi khi bạn khởi động lại Matrix. Sau khi khởi động lại, lưu ý xem xét lại trình đơn này nếu bạn muốn thay đổi bất kỳ cài đặt nào.
Kết quả sẽ có nhiều bề mặt T-Spline không được kết nối với bất kỳ cách nào. Đó không phải là để nói rằng bạn không thể tìm thấy một cách để kết nối chúng khi làm việc tại T-Splines. Một cách đơn giản để nghĩ về nó là để chạy lệnh explode vào mục.
Xem xét khác là T-Splines theo dõi bất kỳ thông tin cắt nào từ các đối tượng NURBS. Nói cách khác, nếu một mục đã được phân chia hoặc trim và sau đó chuyển đổi thành T-Spline, bề mặt T-Spline mới sẽ xuất hiện như nó đã làm trước khi bị tách hoặc trang trí. Về lý thuyết, tất cả các bề mặt trong Ma trận bắt đầu như hình vuông.
17.2/ Độ phân giải cao của đường tròn
Phóng to hình. Bạn sẽ thấy rằng nó bao gồm nhiều ô vuông cực nhỏ xếp thành hình dạng của một vòng tròn. Khi bạn phóng to ra đủ. Để chứng minh rõ hơn về cách này liên quan đến Matrix, hãy thử chuyển đổi một bề mặt tròn phẳng thành một T-Spline. Bề mặt T-Spline sẽ nhớ rằng nó được sinh ra một hình vuông và không thể che dấu dưới mặt tiền hình tròn. Kết quả sẽ là một mặt phẳng T-Spline. Điều này là quan trọng khi bạn cố gắng mang lại các bề mặt vào T-Splines từ Matrix.
Tiếp theo, hãy xem xét các đối tượng booleaned là polysurfaces, vì vậy hãy tính. Một lần nữa, bạn sẽ cần phải làm nổ và chuyển đổi các bề mặt riêng – và thậm chí sau đó, bạn sẽ cần phải tìm cách để đặt tất cả chúng lại với nhau một lần nữa.
17.3/ Chuyển đổi một mặt phẳng đơn giản từ Matrix đến T-Splines
Nếu bạn muốn chuyển đổi một mặt phẳng đơn giản từ Matrix đến T-Splines. Đây là một mẹo để tạo ra mặt phẳng một cách cụ thể mà sẽ gợi ra kết quả dự đoán. Hãy trở lại để suy nghĩ về một bề mặt T-Spline như một bề mặt Degree 3. Biết điều này cho phép bạn dự đoán xây dựng lại bề mặt bằng cách xác định trước bao nhiêu hàng cạnh bạn muốn ở cả hai hướng U & V.
- Bắt đầu bằng cách tạo mặt phẳng từ Matrix’s Surface menu.X
- Xác định cách các mặt bạn muốn có theo hướng U và V. Có 4 mặt theo hướng U và 6 cái theo hướng V .
- Thêm số 3 vào các giá trị. Nói cách khác, tạo lại bề mặt với 7 cái trong hướng U và 9 cái theo hướng V.
- Khi đã tạo lại mặt phẳng, chuyển mục thành T-Spline và viola.
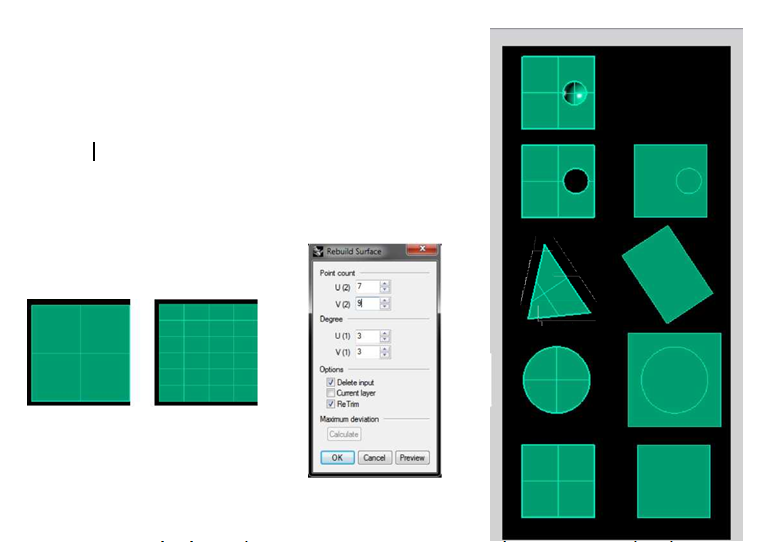
Hộp thoại Rebuild Surface
Khi chuyển đổi các đối tượng từ Matrix thành T-Splines, bề mặt đơn giản là tốt nhất. Nếu không, làm việc trực tiếp trong T-Splines từ get-go. Việc sử dụng phổ biến nhất cho nút ‘’Convert to T-Spline’ là khi bạn đang làm việc tại T-Splines và cần phải chuyển đổi các đối tượng Matrix, nhưng sau đó nhận ra rằng mình cần phải quay trở lại T-Splines cho một vài điều chỉnh.
18/ Kết hợp T-Splines với phần mềm Matrix
18.1/ T-Splines
18.1.1/ Giới thiệu
T-Splines là một công cụ thú vị và mạnh mẽ cho mô hình trong Matrix. Quy trình làm việc mới này là rất khác so với phương pháp NURBS truyền thống và cung cấp nhiều lợi ích to lớn. Hai công nghệ sẽ cho phép bạn thiết kế và tạo ra đồ trang sức mà chỉ giới hạn bởi trí tưởng tượng của bạn. Những thiết kế này sau đó có thể dễ dàng chuyển đổi trở lại bề mặt NURBS và bạn có thể tiếp tục làm việc trên thiết kế của bạn với các công cụ Matrix truyền thống. Tạo bề mặt hình thức miễn phí và hình dạng hệ thống trong T-Splines thêm vào thư viện của bạn, các công cụ và cho phép bạn nhanh chóng khám phá hình dạng, đẩy và kéo chúng cho đến khi chúng phù hợp.
18.1.1/ Bản chất
T-Splines là một công cụ mô hình đa giác. Các đối tượng cơ bản được sử dụng trong mô hình đa giác là một đỉnh hoặc một điểm. Có hai đỉnh và kết nối chúng với một đường thẳng, được gọi là một cạnh. Ba đỉnh nối với nhau bằng cạnh trở thành một hình tam giác. Bốn đỉnh nối với nhau bằng cạnh trở thành hình tứ giác. Bây giờ tạo ra một nhóm các hình tứ giác được kết nối bởi các cạnh và bạn có 1 lưới. Khung cơ bản này là bản chất của T-Splines.
A T-Spline là một bề mặt đại diện sử dụng đa giác. Các đa giác có thể được hiển thị theo một trong hai phương pháp hiển thị khác nhau; Box Mode hoặc Smooth Box/Smooth.
Nút cuối cùng của hàng cuối của H.U.D. Smooth Mode thể hiện chính xác hơn của mô hình T-Spline trong khi Box Mode là 1 cách nhanh chóng, không mượt để hình dung T-Spline và rất hữu ích khi
Làm việc bởi vì rất dễ xác định các chi tiết cụ thể của môi ình bạn muốn thao tác. Bạn sẽ thường làm việc trong Box Mode.
Các T-Splines tích hợp với mô hình Nurbs truyền thống và các lợi ích từ phương pháp tiếp cận hệ thống mới để mô hình hóa.
Thật ra, 1 bề mặt T-Spline sẽ được quan sát ở 2 chế độ; Box Mode hoặc Smooth Mode. Box Mode rất đơn giản, không mượt để xem bề mặt T-Spline. Trong khi Smooth Mode thể hiện chính xác hơn bề mặt T-Spline thực tế. Khi làm việc, bạn sẽ chuyển đổi giữa 2 chế độ này – thường làm việc trên Box Mode để tạo thay đổi và chuyển đổi giữa Smooth Mode để xem sự khác biệt.